风云老师精华文章:
最新精华文章:1,几何证明中的一套底层逻辑
2,高考中涉及新概念新定义的压轴题会对中小学数学学习提出哪些考验
3,立体几何公理化体系
中小学篇:
1,在没有培训的时代,该如何规划中小学数学学习呢?该如何规避一些典型误区?
2,学数学自学提前学,该选择什么样的教材,该选择什么样的课外书???
3,数学学习方法论
4,究竟什么才是数学学习的最重要的基本功?????
5,写给数学牛蛙的一些建议
6,为什么你的孩子从小就学不好数学?写给数学差生和家长的一些建议。
小学篇:
1,小学数学究竟该学什么?培优的大方向究竟在哪里?
2,小学的加减乘除计算训练对中考高考究竟有多少影响?
3,小学数学的几何这一块究竟该怎么学,风云老师为你划重点和核心!
4,小学数学中有哪些内容其实并不重要?
5,职业数学家出的一份小学数学试卷(不断更新中,已更新至21题)
6,风云老师讲除法原理
中学篇:
1,中学数学究竟该学什么?中学数学培优的大方向在哪里?
2,初高中的几何究竟该怎么学??风云老师为你传授绝世神功!!!
3,中学几何之最高境界——复数方法
4,高考非常难,而中考却简单的新形势下,该如何整体规化初高中数学学习??
5,几何证明中的一套底层逻辑
这一节最大的糟点就是不讲推导过程,直接给出公式,像正方体,长方体,圆柱这种非常简单的体积公式直接给出也就罢了,毕竟这种简单立体图形的体积公式好理解,但是像棱锥圆锥和棱台圆台的体积公式居然也直接给出,就有点乱来了。

用倒水实验验证之后,直接给出圆锥的体积公式,那是小学五六年级的水平,小学数学课本就是这么教的。小学课本好歹还有倒水实验作启发,到了高中课本连实验启发都没了,直接就给公式,这么教就不太像话了。在完全不知道这些体积公式为什么成立的前提下,让学生直接接受这些公式,目的是什么?我可以很明确的告诉你,99.9999%的学生在现实生活中根本不会用到这些体积公式?
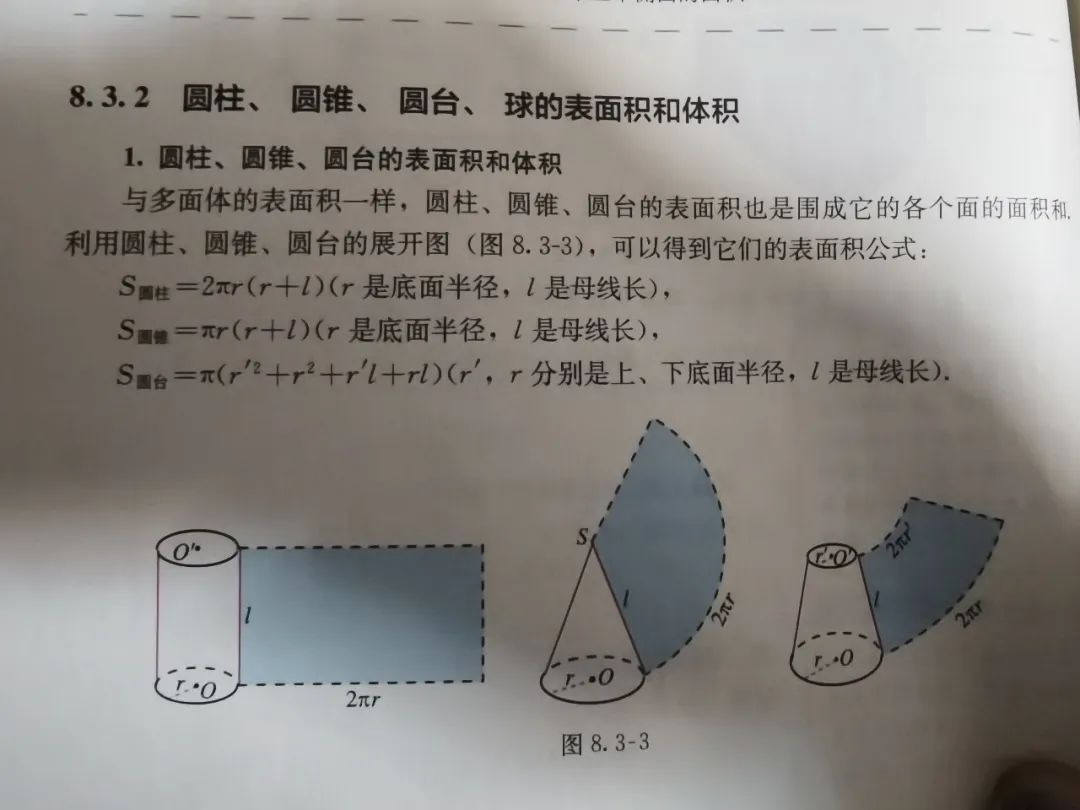
如果知道了母线和底面半径,连稍微厉害点的小学生都会求圆柱和圆锥的表面积,一个个地罗列出这些圆柱和圆锥的表面积公式,意义是什么呢?
至于圆台的表面积,里面的这个侧面积是需要推导的,推导也不难,为什么不讲清楚直接就给公式呢?前面说过了,学这些公式本身根本没什么用处,就高中知识体系而言,因为没有涉及到积分学,这些体积表面积公式本身根本没什么内涵和关联,所以学这些公式本身远远不如学公式的推导来得重要。
前面提到的圆台棱台的体积公式也可以由圆锥棱锥体积公式推导得出,推导过程也并不困难,为什么不教学生推导过程呢?为什么要捡了芝麻丢了西瓜呢?接下来,教材直接粗暴地给出了球的表面积公式,然后运用球表面积公式,锥体体积公式和穷竭法推导出球体体积公式。但是这种推导对普通学生而言是较难理解的,而且学生根本不知道球的表面积公式是怎么来的。既然球的表面积公式可以直接粗暴地给出,那费那么多精力推导球体体积公式还有什么必要呢?干脆也直接给出算了
前面推导圆台表面积公式,用锥体体积推导台体体积公式,这些较简单的推导不讲(后面讲立体几何定理的时候才以例题的形式出现),后面这个较难理解的球体积公式推导却花不小篇幅讲解,这种安排就是非常不合理,完全不考虑教材内容难度的渐进性。
表面积体积这一章节许多内容是以锥体体积公式为前提的,那么教材怎么推导锥体体积公式呢?在这一节最后的探究与发现栏目中,教材居然利用祖暅原理和棱柱体积公式推导出锥体体积公式。首先介绍祖暅原理:两个同高的立体,如在等高处的截面积相等,则体积相等。
第一步,把三棱柱剖成三个三棱锥,利用祖暅原理论证这三个三棱锥体积相等,从而得到三棱锥的体积公式
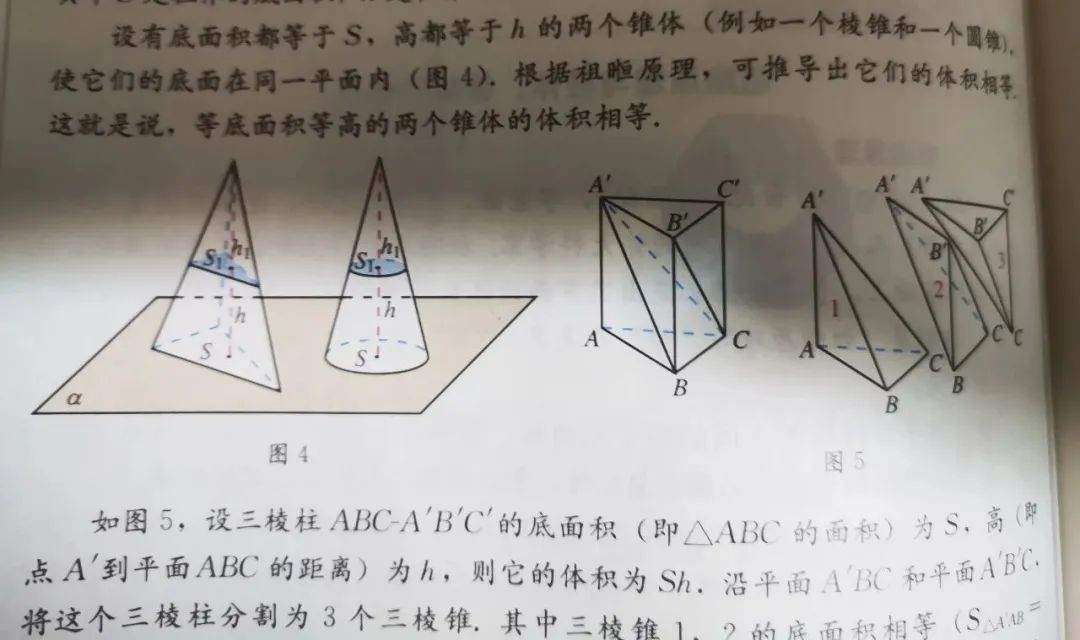
第二步,利用祖暅原理和三棱锥的体积公式,得到圆锥的体积公式。
但是,利用祖暅原理和棱柱体积公式推导出锥体体积公式,这是很偏很小道的技巧,这不是什么基本的东西,这种推导过程根本不适合写入教材供高中生学习。这样的内容安排是非常不合理的。我后面还会讲到为什么?相比较之下,人教版高中数学教材B版对体积表面积这一块的内容安排就有很大的进步,比如,B版就立刻给出了台体体积的推导过程
再比如,讲表面积的时候,没有单纯的列公式,而是指出求表面积的方法。

但是,B版和A版一样,利用祖暅原理和棱柱体积公式推导出锥体体积公式,最后再利用祖暅原理和锥体体积公式推导出球体体积公式。而且B版不是把这些内容放在探究与发现栏目,而是作为教材正文内容独立列一个小节讲解。
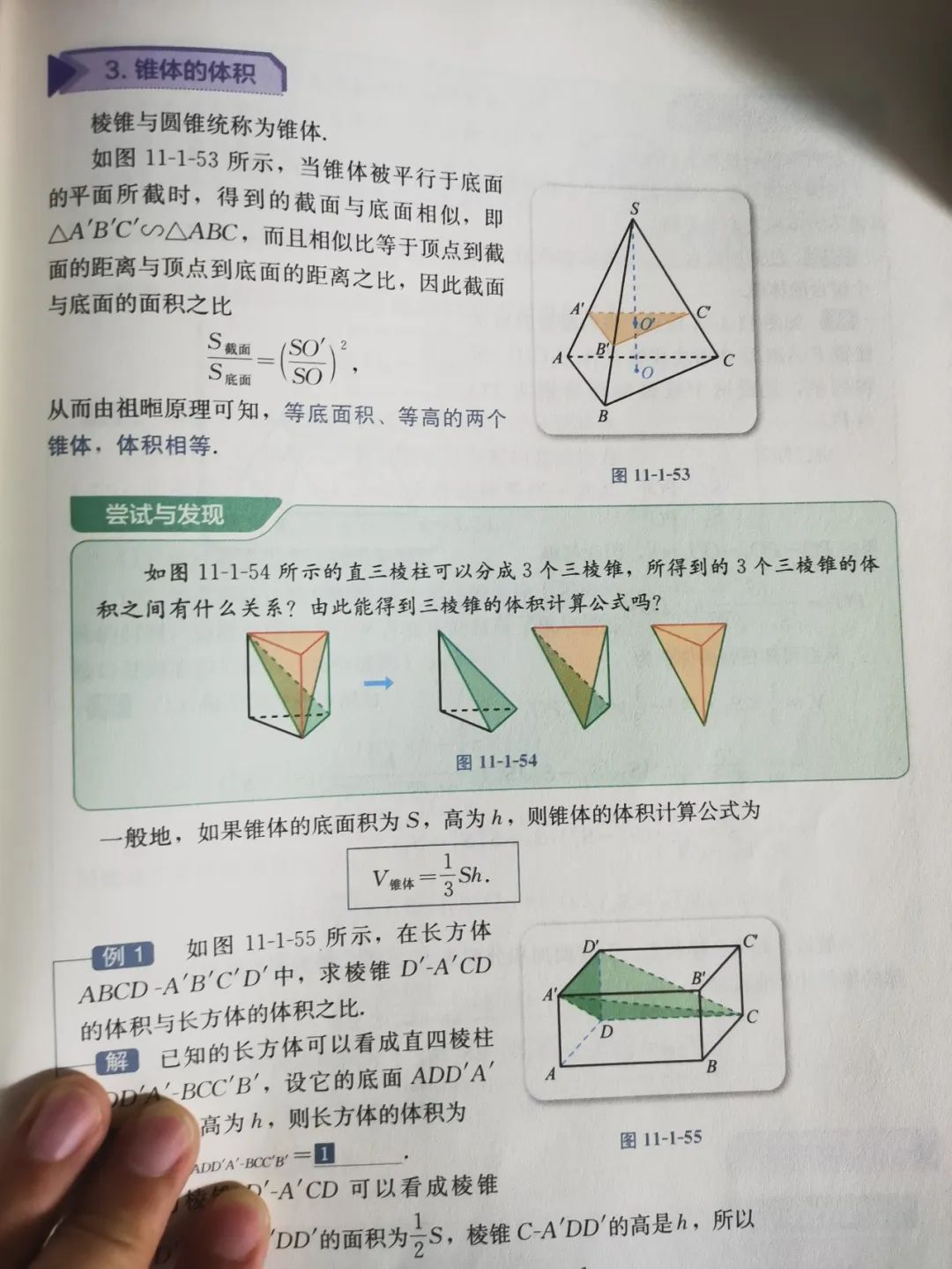

前面讲过了用祖暅原理作的这些推导过程,这些都是很偏很小道的技巧,不是基本的东西,这种推导过程根本不适合写入教材正文供高中生学习。可能有人会问,既然祖暅原理及其应用不适合作为中学教材内容,是否有更好的替代物?
当然有!
其实讲求面积和体积等这些内容时,正是中学生接触积分思想的绝好时机,这是给中学生启蒙积分思想的绝好范例。看看《中小学数学要义》是怎么讲锥体和球体体积的。
实际上,《中小学数学要义》把锥体和球体体积放在数列这一章,很多人可能不理解,为什么看似属于立体几何的内容要放在数列这一章呢?
因为等差数列求和,与求梯形面积可以作非常漂亮的类比,甚至连公式都非常相似。


我们知道等差数列求和再往前一步就是平方数列求和,那这种平方数列求和会对应求什么图形的面积或体积呢?正好对应抛物线围成的曲边三角形求面积和求锥体体积,下面是具体的求解过程: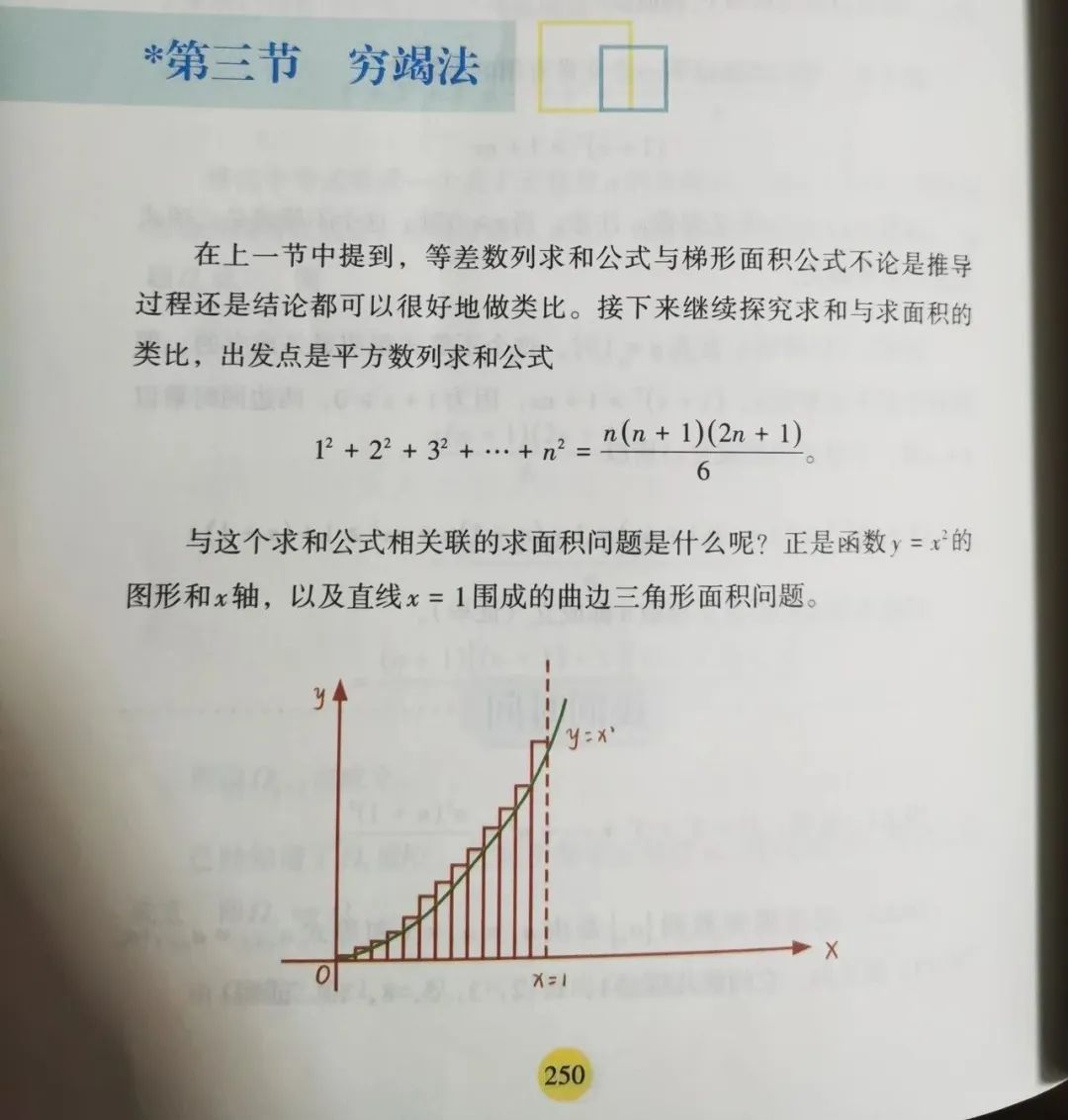

在这一节的习题中,我们还引导读者用类似的方法求出球体的体积。
这种用平方数列求和公式和穷竭法得到面积体积公式的方法是非常核心非常基本的方法,已经充分体现微积分中的积分思想,和微积分教材中积分的定义已经非常非常接近了。中学生学习掌握这种方法就是打开了一扇通往微积分高等数学的大门。教材中同样长的篇幅,同样的学习难度,可以写运用祖暅原理推导锥体球体体积,也可以写利用平方数列求和公式和穷竭法推导锥体球体体积,但学习效果差别可能是萤虫之光和日月的差别。所以,我认为教材更合理的安排是,体积表面积这一块专题很多单纯是给出公式的内容完全可以不必讲,甚至不必单独列体积表面积这一章节。至于锥体球体的体积公式,如果要讲,可以放入数列这一章,单独开一节讲穷竭法求锥体球体的体积公式,顺便给中学生作一次积分思想的启蒙。
总之,教材内容的编写是门大学问,非常考验编写者的数学格局和视野。最后推荐一套非常精彩的课外书 《what if 1,2》 《How to》这套书里面讨论了各种脑洞大开的有趣问题,非常能满足孩子的好奇心,




我家小孩和亲戚家几个小孩每个孩子读这套书都读得津津有味,爱不释手,我相信没几个孩子能抵挡得住这套书的诱惑。这种类型的书非常适合那些不喜欢阅读的孩子,用来培养阅读兴趣。